Lambert Beer Law: A Complete Guide for Scientists

Have you ever wondered how scientists measure the concentration of pollutants in water, or determine the amount of active ingredient in a medication? The answer often lies in a fundamental principle of light absorption known as the Lambert-Beer Law. This powerful law provides a straightforward relationship between the concentration of a substance and the amount of light it absorbs, making it an indispensable tool in fields ranging from chemistry and biology to environmental science and manufacturing.

This guide will walk you through everything you need to know about the Lambert-Beer Law. We will explore its historical roots, break down its mathematical formula, and examine its practical applications. You will also learn about the factors that can cause deviations from the law and work through practical examples to solidify your understanding. By the end, you’ll have a clear grasp of why this principle is so crucial for quantitative analysis.

What is the Lambert-Beer Law?

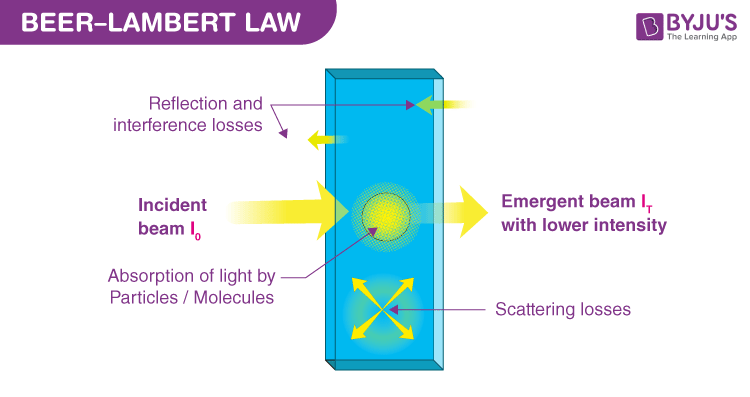
The Lambert-Beer Law, also known as the Beer-Lambert Law or Beer’s Law, is a principle that relates the attenuation of light to the properties of the material through which the light is traveling. In simpler terms, it states that the amount of light absorbed by a solution is directly proportional to both the concentration of the absorbing substance and the distance the light travels through the solution (the path length).

This principle is the foundation of spectrophotometry, a technique used to measure how much a chemical substance absorbs light by measuring the intensity of light as a beam of light passes through a sample solution. By measuring the absorbance, scientists can accurately calculate the concentration of the substance in the solution.

A Brief History: Lambert and Beer

The law is named after two key scientists who laid its groundwork.

• Johann Heinrich Lambert (1728–1777): In 1760, this Swiss polymath published his work on photometry. He discovered that the absorbance of light by a sample is directly proportional to the thickness (path length) of the sample. Essentially, the thicker the material, the more light it absorbs. This became known as Lambert’s Law.
• August Beer (1825–1863): Nearly a century later, in 1852, German physicist and mathematician August Beer expanded on Lambert’s findings. He established that the absorbance of a solution is also directly proportional to the concentration of the dissolved substance. This finding, known as Beer’s Law, completed the picture.

By combining their discoveries, the scientific community formulated the unified Lambert-Beer Law, which remains a cornerstone of analytical chemistry today.

The Components of the Lambert-Beer Law

To fully understand the law, it’s essential to break down its core components: absorbance, concentration, path length, and molar absorptivity.

Absorbance (A)

When light passes through a solution, some of it is absorbed by the molecules within it, and the rest is transmitted through. Absorbance is a measure of the quantity of light that is absorbed by the sample. It is a dimensionless quantity and is sometimes referred to as optical density.

Absorbance is related to transmittance (T), which is the fraction of incident light that passes through the sample. The relationship is logarithmic:
A = -log(T)
Where T is often expressed as a percentage (T%) or a decimal (T = I / I₀, where I is the intensity of transmitted light and I₀ is the intensity of incident light).

Concentration (c)

Concentration refers to the amount of a substance (the solute) dissolved in a given volume of a solution (the solvent). In the context of the Lambert-Beer Law, concentration is typically expressed in moles per liter (mol/L or M). The law demonstrates a linear relationship between absorbance and concentration: as concentration increases, absorbance increases proportionally, assuming other factors remain constant.

Path Length (b)

The path length is the distance that light travels through the solution. This is determined by the width of the container holding the sample, which is called a cuvette. Standard cuvettes have a path length of 1.00 cm, which simplifies calculations. Like concentration, path length is directly proportional to absorbance—doubling the path length will double the absorbance.

Molar Absorptivity (ε)

Molar absorptivity, also known as the molar extinction coefficient, is a constant that measures how strongly a chemical species absorbs light at a specific wavelength. It is a unique physical property of a substance. The value of ε is dependent on the chemical nature of the substance, the solvent used, the temperature, and the wavelength of light. Its units are typically liters per mole-centimeter (L mol⁻¹ cm⁻¹ or M⁻¹ cm⁻¹). A high molar absorptivity value indicates that the substance is very effective at absorbing light at that particular wavelength.

The Mathematical Formulation

The Lambert-Beer Law is expressed by the following equation:

A = εbc

Where:

• A is the absorbance (no units)
• ε (epsilon) is the molar absorptivity (M⁻¹cm⁻¹)
• b is the path length of the cuvette (cm)
• c is the concentration of the substance (M)

This simple equation allows us to calculate the concentration of a sample if we know its absorbance, path length, and molar absorptivity. In practice, a calibration curve is often created by measuring the absorbance of several solutions of known concentrations. Plotting absorbance versus concentration yields a straight line, and the concentration of an unknown sample can be determined by measuring its absorbance and finding the corresponding concentration on the curve.

Factors Affecting the Lambert-Beer Law

While incredibly useful, the Lambert-Beer Law is not perfect. It works best under specific ideal conditions, and deviations can occur. Understanding these limitations is crucial for accurate absorbance measurement.

1. High Analyte Concentrations

The linear relationship between absorbance and concentration holds true for dilute solutions. At high concentrations (typically > 0.01 M), molecules can begin to interact with each other, which may alter their ability to absorb light. These solute-solute interactions can change the molar absorptivity of the substance, causing the calibration curve to bend and deviate from linearity.

2. Chemical Deviations

Chemical reactions within the solution can also lead to deviations. If the absorbing substance undergoes association, dissociation, or reaction with the solvent, the concentration of the species that is actually absorbing light may change. For example, changes in pH can alter the chemical form of an indicator, causing a shift in its absorbance spectrum and a deviation from the law.

3. Polychromatic Radiation

The Lambert-Beer Law is strictly valid only when using monochromatic light—that is, light of a single wavelength. Most spectrophotometers use a monochromator to isolate a narrow band of wavelengths. However, if this band is too wide (polychromatic), deviations can occur. Different wavelengths are absorbed to different extents, and the instrument will measure an average absorbance, leading to a non-linear relationship.

4. Stray Light Effects

Stray light is any light that reaches the detector without passing through the sample. This can come from reflections within the instrument or leaks from the outside. Stray light is particularly problematic at high absorbance values, where very little light is transmitted through the sample. It can cause absorbance readings to be lower than they actually are, leading to significant errors.

5. Turbidity

The law assumes the solution is clear and non-scattering. If the sample is turbid (cloudy) due to suspended particles, light will be scattered in addition to being absorbed. This scattered light does not reach the detector and is incorrectly measured as absorbance, leading to falsely high readings. Samples must be filtered or centrifuged to remove turbidity before measurement.

Practical Applications of the Lambert-Beer Law

The Lambert-Beer Law is applied across numerous scientific and industrial fields. Here are some key examples:

• Water Quality Monitoring: Environmental scientists use spectrophotometry to measure the concentration of pollutants like nitrates, phosphates, and heavy metals in water samples. For instance, the concentration of iron in drinking water can be determined by adding a reagent that forms a colored complex with iron, then measuring its absorbance.
• Pharmaceutical Analysis: In the pharmaceutical industry, UV-Vis spectroscopy is a standard method for determining the concentration of active pharmaceutical ingredients (APIs) in drug formulations. This ensures that medications contain the correct dosage.
• Biochemical Assays: The law is fundamental to many biochemical assays. The Bradford and Lowry assays, for example, use colorimetric reactions to quantify protein concentrations. Enzyme activity can also be measured by monitoring the rate of change in absorbance as a substrate is converted to a product.
• Food and Beverage Industry: Quality control in the food industry often relies on spectrophotometry. For example, the color and clarity of beer and wine are measured to ensure consistency. The law can also be used to determine the concentration of compounds like caffeine in beverages.
• Clinical Chemistry: In medicine, the law is used to measure the concentration of various substances in blood and urine, such as glucose, cholesterol, and hemoglobin, aiding in the diagnosis of diseases.

Quantitative Problems and Solutions

Let’s apply the Lambert-Beer Law to solve a few problems.

Problem 1

A solution has an absorbance of 0.750 at a wavelength of 480 nm in a 1.00 cm cuvette. If the molar absorptivity of the solution at this wavelength is 8400 M⁻¹cm⁻¹, what is the concentration of the solution?

Solution:
Start with the Lambert-Beer Law equation: A = εbc
Rearrange to solve for concentration (c): c = A / (εb)
Substitute the given values:
c = 0.750 / (8400 M⁻¹cm⁻¹ × 1.00 cm)
c ≈ 8.93 x 10⁻⁵ M

Problem 2

A colored compound has a molar absorptivity of 5000 M⁻¹cm⁻¹ at 520 nm. If a solution containing this compound has a concentration of 2.5 x 10⁻⁵ M, what is the absorbance of the solution in a 2.00 cm cuvette?

Solution:
Use the Lambert-Beer Law equation directly: A = εbc
Substitute the given values:
A = 5000 M⁻¹cm⁻¹ × 2.00 cm × 2.5 x 10⁻⁵ M
A = 0.250

Problem 3

The transmittance of a solution is measured to be 30.0% when placed in a spectrophotometer. If the path length of the cuvette is 1.00 cm and the molar absorptivity is 4500 M⁻¹cm⁻¹, calculate the concentration of the solution.

Solution:
First, convert transmittance (T) to absorbance (A).
T = 30.0% = 0.300
A = -log(T) = -log(0.300) ≈ 0.523
Now, use the Lambert-Beer Law rearranged to solve for concentration: c = A / (εb)
Substitute the values:
c = 0.523 / (4500 M⁻¹cm⁻¹ × 1.00 cm)
c ≈ 1.16 x 10⁻⁴ M

Advancing Science with Light Absorption

The Lambert-Beer Law provides an elegant and powerful connection between light absorption and concentration. Its simplicity and broad applicability have cemented its role as a fundamental tool in modern science. From ensuring the purity of our water to verifying the potency of our medicines, its impact is felt in countless aspects of our daily lives. While it is important to be mindful of its limitations, a solid understanding of this law opens the door to a wide array of analytical techniques that continue to drive innovation and discovery.

Frequently Asked Questions (FAQ)